Chapter 4 Physics and Modeling of the Airway
I the Gas Laws
A Ideal Gases
Perhaps the most important law of gas flow in airways is the ideal (or perfect) gas law, which can be written as follows1:
P = pressure of gas (pascals or mm Hg)
V = volume of gas (m3 or cm3 or mL)
n = number of moles of the gas in volume V
R = gas constant (8.3143 J g-mol−1·K−1, assuming P in pascals, V in m3)
One mole of gas contains 6.023 × 1023 molecules, and this quantity is termed Avogadro’s number. One mole of an ideal gas takes up 22.4138 L at standard temperature and pressure (STP); standard temperature is 273.16 K, and standard pressure is 1 atmosphere (760 mm Hg).1 Avogadro also stated that equal volumes of all ideal gases at the same temperature and pressure contain the same number of molecules.
The ideal gas law incorporates the laws of Boyle and Charles.1 Boyle’s law states that, at a constant temperature, the product of pressure and volume (P × V) is equal to a constant. Consequently, P is proportional to 1/V (P ∝ 1/V) at constant T. However, gases do not obey Boyle’s law at temperatures approaching their point of liquefaction (i.e., the point at which the gas becomes a liquid).
Charles’ law states that, at a constant pressure, volume is proportional to temperature (i.e., V ∝ T at constant P). Gay-Lussac’s law states that, at a constant volume, pressure is proportional to temperature (i.e., P ∝ T at constant V).1 Often, these two laws are shortened for convenience to Charles’ law. When a gas obeys both Charles’ law and Boyle’s law, it is said to be an ideal gas and obeys the ideal gas law.
In clinical situations, gases are typically mixtures of several “pure” gases. Quantifiable properties of mixtures may be determined using Dalton’s law of partial pressures. Dalton’s law states that the pressure exerted by a mixture of gases is the sum of the pressures exerted by the individual pure gases1,2:
where PA, PB, and PC are the partial pressures of pure ideal gases.
B Nonideal Gases: The van der Waals Effect
Ideal gases have no forces of interaction, but real gases have intermolecular attraction, which requires that the pressure-volume gas law be rewritten as follows1,2:
P = pressure of gas (pascals or mm Hg)
V = volume of gas (m3 or cm3 or mL)
n = number of moles of the gas in volume V
R = gas constant (8.3143 J g- mol−1·K−1, assuming P in pascals, V in m3)
The values of a and b for a given gas may be found in physical chemistry textbooks and other sources.1–5 This formulation, provided by van der Waals, accounts for intramolecular forces fairly well.
C Diffusion of Gases
Clinically, diffusion of gases through a membrane is most applicable to gas flow across lung and placental membranes. The most commonly used relation to govern diffusion is Fick’s first law of diffusion, which states that the rate of diffusion of a gas across a barrier is proportional to the concentration gradient for the gas. Fick’s law may be expressed mathematically as follows6:
Flux = the number of molecules crossing the membrane each second (molecules/cm2/s)
ΔC = the concentration gradient (molecules/cm3)
ΔX = the diffusion distance (cm)
Because gases partially dissolve when they come into contact with a liquid, Henry’s law becomes important in some instances. It states that the mass of a gas dissolved in a given amount of liquid is proportional to the pressure of the gas at constant temperature. As a result, the gas concentration (in solvent) is equal to a constant × P (at constant T).1
D Pressure, Flow, and Resistance
Flow (i.e., the rate of flow) is equal to the change in pressure (pressure drop or pressure difference) divided by the resistance experienced by the fluid. For example, if the flow is 100 mL/s at a pressure difference of 100 mm Hg, the resistance is 100 mm Hg/100 mL/s, or 1 mm Hg/mL/s. In laminar flow systems only, the resistance is constant, independent of the flow rate.7,8
An important formula that quantifies the relationship of pressure, flow, and resistance in laminar flow systems is given by the Hagen-Poiseuille equation. Poiseuille’s law states that the fluid flow rate through a horizontal straight tube of uniform bore is proportional to the pressure gradient (ΔP), and the fourth power of the radius (π) and is related inversely to the viscosity of the gas (µ, in g/cm·s) and the length of the tube (L, in cm). This law, which is valid for laminar flow only, may be stated as follows7,8:
See the discussion of laminar flow in Section II for further details.
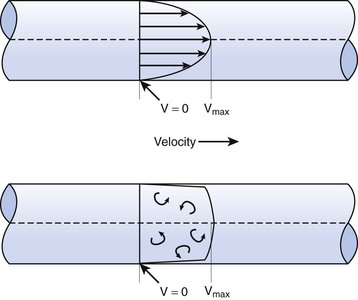
When the flow rate exceeds a critical velocity (the flow velocity below which flow is laminar), the flow loses its laminar parabolic velocity profile, becomes disorderly, and is termed turbulent (Fig. 4-1). If turbulent flow exists, the relationship between pressure drop and flow is no longer governed by the Hagen-Poiseuille equation. Instead, the pressure gradient required (or the resistance encountered) during turbulent flow varies as the square of the flow rate. See the discussion of turbulent flow in Section II.
Viscosity, µ, characterizes the resistance within a fluid to the flow of one layer of molecules over another (shear characteristics).7 Blood viscosity is influenced primarily by hematocrit, so that at low hematocrit blood flow is easier—that is, blood is more dilute. The critical velocity at which turbulent flow begins depends on the ratio of viscosity (µ) to density (ρ), which is defined as the kinematic viscosity (υ)—that is, υ = µ/ρ. (This is illustrated with an example in the section on turbulent flow).7–9 The unit for viscosity is g/cm·s (poise). The typical unit for kinematic viscosity is cm2/s.
The viscosity of water is 0.01 poise at 25° C and 0.007 poise at 37° C. The viscosity of air is 183 micropoise at 18° C. Its density (dry) is 1.213 g/L.10
where D0 is a known density of the gas at temperature T0 and pressure P0, and D is the density of the gas at temperature T and pressure P. For dry air at 18° C and 760 mm Hg (atmospheric pressure), D = 1.213 g/L.4
The fall in pressure at points of flow constriction (where the flow velocity is higher) is known as the Bernoulli effect (Fig. 4-2).7,8 This phenomenon is used in apparatus employing the Venturi principle, such as gas nebulizers, Venturi flowmeters, and some oxygen face masks. The lower pressure related to the Bernoulli effect sucks in (entrains) air to mix with oxygen.
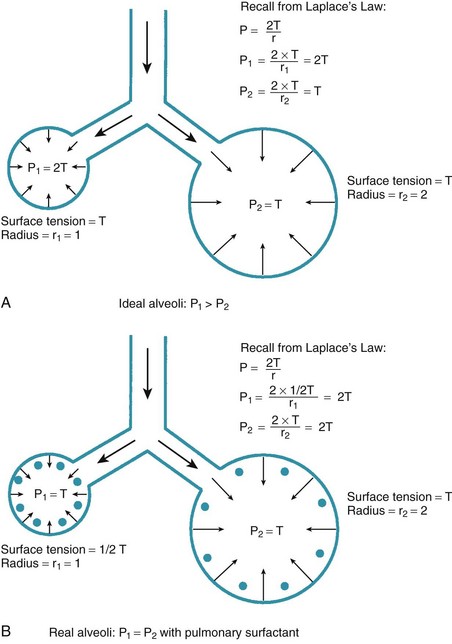
One final consideration that is important in the study of the airway is Laplace’s law for a sphere (Fig. 4-3). It states that, for a sphere with one air-liquid interface (e.g., an alveolus), the relation between the transmural pressure difference, surface tension, and sphere radius is described by the following equation11:
P = transmural pressure difference (dynes/cm2; 1 dyne/cm2 = 0.1 Pa = 0.000751 torr)
T = surface tension (dynes/cm)
E Example: Analysis of Transtracheal Jet Ventilation
Transtracheal jet ventilation (TTJV) has been used to oxygenate and ventilate patients who would otherwise perish because of a lost airway.6 It is a temporizing measure that is used only until an airway can be secured. It is usually employed using equipment commonly available in the operating or emergency room and often using the 50-psi wall oxygen source.6,12–14
1 Analysis
In a TTJV setup consisting of a 14-G angiographic catheter connected to a regulated oxygen source by a 4.5-foot polyvinyl chloride (PVC) tube of 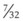 -inch inner diameter (ID), for oxygen flows between 10 and 60 L/min, the resistance was found to be relatively constant between 0.6 and 0.8 psi/L/min.15
-inch inner diameter (ID), for oxygen flows between 10 and 60 L/min, the resistance was found to be relatively constant between 0.6 and 0.8 psi/L/min.15
II Gas Flow
A Laminar Flow
In laminar flow, fluid particles flow along smooth paths in layers, or laminas, with one layer gliding smoothly over an adjacent layer.7 Any tendencies toward instability and turbulence are damped out by viscous shear forces that resist the relative motion of adjacent fluid layers. Under laminar flow conditions through a tube, the flow velocity is greatest at the center of the tube flow and zero at the inner edge of the tube (Fig. 4-4; see also Fig. 4-1). The flow profile has a parabolic shape. Under these conditions in a horizontal tube, the relation between flow, tube, and gas characteristics is given by the Hagen-Poiseuille equation (Equation 5), restated as follows7–9:
Typical units are shown in parentheses. The dot indicates rate of change: V represents volume, and 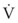 represents the rate of change of volume, or flow rate. Another way of looking at this concept is that, under conditions of laminar flow through a tube of known radius, the pressure difference across the tube is given by the following proportionality (which is also essentially the same as Equation 5):
represents the rate of change of volume, or flow rate. Another way of looking at this concept is that, under conditions of laminar flow through a tube of known radius, the pressure difference across the tube is given by the following proportionality (which is also essentially the same as Equation 5):
B Turbulent Flow
Flow in tubes below the critical flow rate remains mostly laminar. However, at flows greater than the critical flow rate, the flow becomes increasingly turbulent. Under turbulent flow conditions, the parabolic flow pattern is lost, and the resistance to flow increases with flow itself. Turbulence may also be created where sharp angles, changes in diameter, and branches are encountered (Fig. 4-5). The flow-pressure drop relationship is given approximately by the following equation7,8:
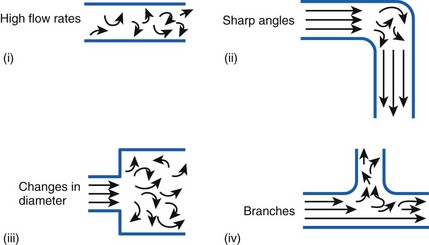
Figure 4-5 Turbulent flow. Four circumstances likely to produce turbulent flow.
(From Nunn JF: Nunn’s applied respiratory physiology, ed 4, Stoneham, MA, 1993, Butterworth-Heinemann.)
1 Reynolds Number Calculation Example
The Reynolds number (Re) represents the ratio of inertial forces to viscous forces.7,8,16 It is useful because it characterizes the flow through a long, straight tube of uniform bore. It is a dimensionless number having the following form:
Typical units are shown in brackets. For tubes that are long compared with their diameter (i.e., length ÷ diameter > 0.06 × Re),8 the flow is laminar when Re is less than 2000. For shorter tubes, flow is turbulent at Re values as low as 280.
When a tube’s radius exceeds its length, it is an orifice; flow through an orifice is always turbulent. Under these conditions, the flow is influenced by the density rather than the viscosity of the fluid.17 This characteristic explains why heliox (e.g., the mixture of 70% He and 30% O2) flows better in a narrow edematous glottis: as the following data suggest, helium has a very low density and thus presents less resistance to flow through an orifice.
| Viscosity at 20° C | Density at 20° C | |
|---|---|---|
| Helium | 194.1 micropoise | 0.179 g/L |
| Oxygen | 210.8 micropoise | 1.429 g/L |
With this information, one can calculate the Reynolds number:
Because this number greatly exceeds 2000, flow is probably quite turbulent.
C Critical Velocity
The critical velocity is the point at which the transition from laminar to turbulent flow begins. This point is reached when Re becomes the critical Reynolds number, Recrit. Critical velocity, the flow velocity below which flow is laminar, is calculated by the following equation8:
where Recrit = 2000 for circular tubes.
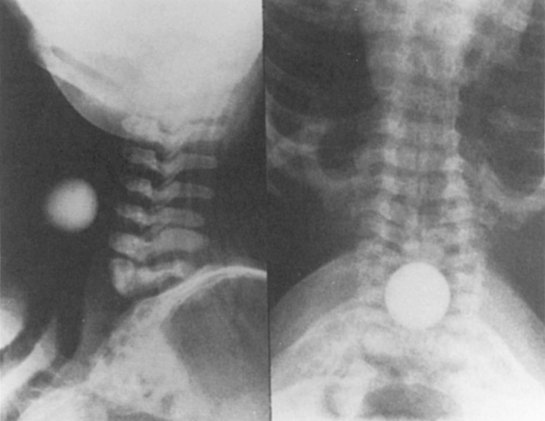
D Flow Through an Orifice
Flow through an orifice (defined as flow through a tube whose length is smaller than its radius) is always somewhat turbulent.17 Clinically, airway-obstructing conditions such as epiglottitis or swallowed obstructions are often best viewed as breathing through an orifice (Fig. 4-6). Under such conditions, the approximate flow across the orifice varies inversely with the square root of the gas density:
This is in contrast to laminar flow conditions, in which gas flow varies inversely with gas viscosity. The viscosity values for helium and oxygen are similar, but their densities are very different (Table 4-1). Table 4-2 provides useful data to allow comparison of gas flow rates through an orifice.18
TABLE 4-1 Viscosity and Density Differences of Anesthetic Gases
| Viscosity at 300 K | Density at 20° C | |
|---|---|---|
| Air | 18.6 µPa × s | 1.293 g/L |
| Nitrogen | 17.9 µPa × s | 1.250 g/L |
| Nitrous oxide | 15.0 µPa × s | 1.965 g/L |
| Helium | 20.0 µPa × s | 0.178 g/L |
| Oxygen | 20.8 µPa × s | 1.429 g/L |
Data from Haynes WM: CRC Handbook of chemistry and physics, ed 91, Boca Raton, FL, 2010, CRC Press, and Streeter VL, Wylie EB, Bedford KW: Fluid mechanics, ed 9, New York, 1998, McGraw-Hill.
1 Helium-Oxygen Mixtures
The low density of helium allows it to play a significant clinical role in the management of some forms of airway obstruction.19–22 For instance, Rudow and colleagues described the use of helium-oxygen (heliox) mixtures in a patient with severe airway obstruction related to a large thyroid mass (see next section for clinical examples).18
Although the use of heliox mixtures in patients with upper airway obstruction has met with considerable success, the hope that this approach would also work well for patients with severe asthma has not been borne out. In a systematic review of seven clinical trials involving 392 patients with acute asthma, the authors cautioned that “existing evidence does not provide support for the administration of helium-oxygen mixtures to emergency department patients with moderate-to-severe acute asthma.”23 A similar study noted that “heliox may offer mild-to-moderate benefits in patients with acute asthma within the first hour of use, but its advantages become less apparent beyond 1 hour, as most conventionally treated patients improve to similar levels, with or without it”; however, the authors suggested that its effect “may be more pronounced in more severe cases.” They concluded that “there are insufficient data on whether heliox can avert endotracheal intubation, or change intensive care and hospital admission rates and duration, or mortality.”24
2 Clinical Vignettes
Rudow and colleagues reported the following clinical illustration of heliox therapy.18 A 78-year-old woman with both breast cancer and ophthalmic melanoma developed airway obstruction from a thyroid carcinoma that extended into her mediastinum and compressed her trachea. She had a 2-month history of worsening dyspnea, especially when positioned supine. On examination, inspiratory and expiratory stridor was present. The chest radiograph showed a large superior mediastinal mass and pulmonary metastases. A solid mass was identified on a thyroid ultrasound scan. Computed tomography revealed a large mass at the thoracic inlet and extending caudally. Clinically, the patient was exhausted and in respiratory distress.
Another interesting clinical scenario was published by Khanlou and Eiger.25 They presented the case of a 69-year-old woman in whom bilateral vocal cord paralysis developed after radiation therapy. Heliox was successfully used for temporary management of the resultant upper airway obstruction until the patient was able to receive a tracheostomy.
A final clinical vignette was reported by Polaner,26 who used the laryngeal mask airway and an 80 : 20 heliox mixture to administer anesthesia to a 3-year-old boy with asthma and a large anterior mediastinal mass. Clinical management involved an unusual combination of management strategies: the child was kept in the sitting position, spontaneous ventilation with a halothane-in-heliox inhalation induction was used, and airway stimulation was minimized by use of the laryngeal mask airway. However, the author cautioned that cases such as these can readily take a deadly turn, noting that “one must, of course, always be prepared to intervene with either manipulations of patient position in the event of airway compromise (including upright, lateral, and prone) or more aggressive strategies, such as rigid bronchoscopy and even median sternotomy (in the case of intractable cardiovascular collapse), or to allow the patient to awaken if critical airway or cardiovascular compromise becomes evident at any time during the course of the anesthesia.”26
E Pressure Differences
From the analysis of equations governing laminar flow and turbulent flow, the pressure drop along the noncompliant portion of the airway is given approximately by the Rohrer equation27:
1. Effects proportional to gas flow (laminar flow effects)
2. Effects proportional to the square of the gas flow (turbulent flow effects)
F Resistance to Gas Flow
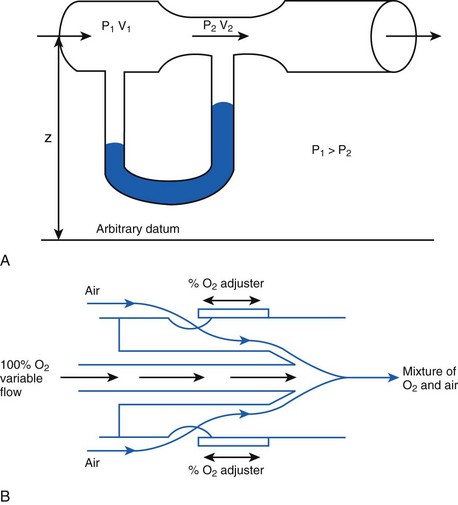
When pressure readings are taken at each end of a horizontal tube with a fluid flowing through it, one notices that they are not identical: The pressure at the distal end of the tube is less than the pressure at the proximal end (with fluid flowing from the proximal to the distal end). This pressure loss is attributable to frictional losses incurred by the fluid when in contact with the inside of the tube. This is analogous to heat losses incurred by resistors in an electrical circuit (Fig. 4-7).
Frictional losses are irreversible; that is, the energy lost cannot be recovered by the fluid and is mostly lost as heat. If the tube is not horizontal, there are additional pressure differences attributable to height differences. The most common relation that describes the flow in a tube is the Bernoulli equation, which is valid for both laminar and turbulent flow8:
g = gravitational constant (9.81 m/s2 or 9.81 N/kg)
P = pressure (pascals or N/m2)
Z = height from an arbitrary point (datum) (m)
Typical units are shown in square brackets. Equation 18 is in units of meters and is termed “meters of head loss.” This is typical of fluid mechanics equations. As mentioned previously, the Bernoulli equation is valid for both laminar and turbulent flow.
1 Endotracheal Tube Resistance
ETTs, like all tubes, offer resistance to fluid flow (Fig. 4-8). However, ETTs do not add external resistance to the normal airway; rather, they act as a substitute for the normal resistance of the airway from the mouth to the trachea, which accounts for 30% to 40% of normal airway resistance.28 This is important because, although mechanical ventilators can overcome impedance to inspiratory flow during extended periods of artificial respiration, they do not augment passive exhalation. Resistance to exhalation through a long, small-diameter ETT, which is compounded by turbulence, can seriously constrain ventilation rate and tidal volume.29,30
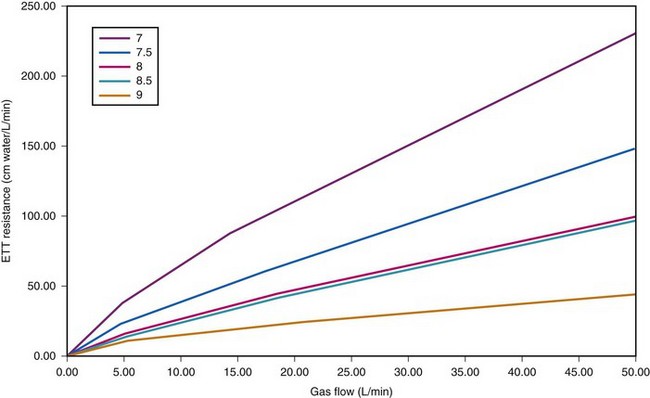
Figure 4-8 Dependence of endotracheal tube (ETT) on flow. The data provided by Hicks in Table 4-3 can be used to show that ETT resistance increases nonlinearly with flow (because of turbulence effects). For pure laminar flow, resistance would be constant, regardless of flow.
The use of the ETT influences respiration in a number of ways. First, it decreases effective airway diameter and therefore increases the resistance to breathing. Resistance is further increased by the curved nature of the tube; resistance measurements are typically about 3% higher than if the tubes were straight.31 Also, the passage from the mouth to the larynx is not a smooth curve and may create additional turbulence. Second, studies show that intubated patients experience decreased peak flow rates (inspiratory and expiratory), decreased forced vital capacity, and decreased forced expiratory volume in 1 second (FEV1).32 However, the tube may paradoxically increase peak flow rates during forced expiration by preventing dynamic compression of the trachea.32 Finally, the tube may cause mechanical irritation of the larynx and trachea that may lead to a reflex constriction of the airway distal to the tube.33
The combination of tube and connector may cause higher resistance than the tube alone. Moreover, because of turbulence at component connections, the total resistance of a system is not necessarily the sum of the resistances of its component parts, especially if sharp-angled connectors are used (see Fig. 4-5).25,34 In addition, humidified gases contribute to slightly higher resistances because of the increased density of moist gas, and the resistance of single-lumen tubes is generally lower than that of double-lumen tubes.35
The resistance associated with ETTs may be reduced by increasing the tube diameter, decreasing tube length, or decreasing the gas density (hence, the occasional use of heliox mixtures). It has been suggested that the presence of an ETT may double the work of breathing in chronically intubated adults and may lead to respiratory failure in some infants.31 Therefore, it is important to use as large an ETT as is practical in patients who exhibit respiratory dysfunction.
ETT resistance can be measured in the laboratory using differential pressure and flow measurement techniques,36,37 most commonly by the method of Gaensler and colleagues.38 Theoretical estimates of resistance under laminar flow conditions can also be obtained by using the Poiseuille equation. In vivo measurements of ETT resistance are generally higher than in vitro measurements, perhaps because of secretions, head or neck position, tube deformation, or increased turbulence.10,39
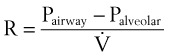
Airway resistance may be established from first principles using Poiseuille’s law if the gas flow is laminar. If gas flow is turbulent, resistance is no longer independent of material properties, and empirical measurements become the only feasible means of characterizing resistance. Intrinsic airway resistance is determined by measuring the transairway pressure—that is, the pressure drop between the airway opening and the alveoli. The following relationship applies40:

Full access? Get Clinical Tree


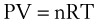 (1)
(1)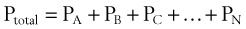 (2)
(2)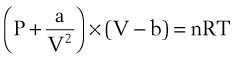 (3)
(3)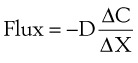 (4)
(4)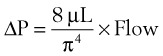 (5)
(5)
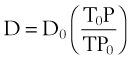 (6)
(6)
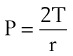 (7)
(7)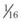 min = 0.5 L.
min = 0.5 L.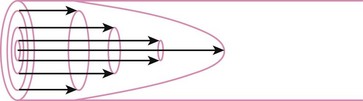
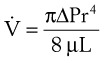 (8)
(8)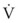 = flow rate (cm3/s)
= flow rate (cm3/s)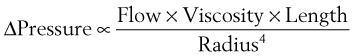 (9)
(9)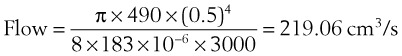 (10)
(10)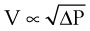 (11)
(11)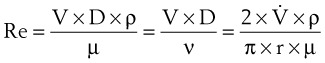 (12)
(12)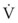 = flow rate (mL/s)
= flow rate (mL/s)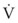 ) = 60 L/min = 1000 mL/s
) = 60 L/min = 1000 mL/s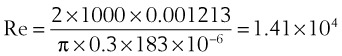 (13)
(13)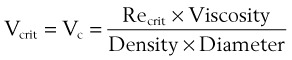 (14)
(14)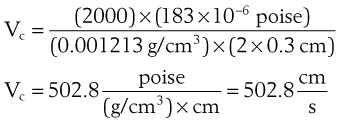 (15)
(15)
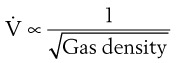 (16)
(16)
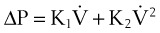 (17)
(17) is small (i.e., with predominantly laminar flow). However, it is known that under conditions of laminar flow, K1 is largely influenced by viscosity rather than density, and K2 (the turbulent term) is influenced primarily by density and not viscosity.
is small (i.e., with predominantly laminar flow). However, it is known that under conditions of laminar flow, K1 is largely influenced by viscosity rather than density, and K2 (the turbulent term) is influenced primarily by density and not viscosity.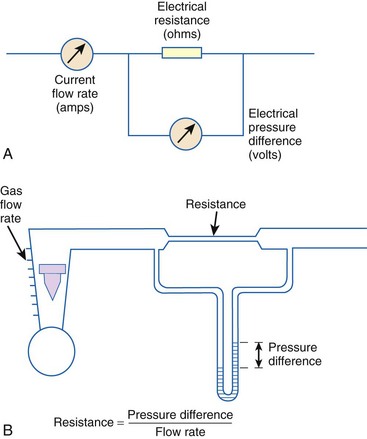
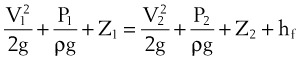 (18)
(18) (19)
(19) = gas flow rate (L/s)
= gas flow rate (L/s)




