Performance of Target-Controlled Infusion Systems



Fig. 9.1
Closed-loop control of propofol infusion aiming to maintain a bispectral value of 80 in a patient receiving sedation for gastrointestinal endoscopy. The infusion was controlled by an automated proportional-integral-differential control algorithm. The initial period showed a big variation in BIS producing a large performance error. The control algorithm was changed with a 20 % increase in the control of “proportional” value (arrow), and this resulted in a lower performance error



Varvel and others have recommended five indices to quantify TCI performance [11].


  1. 1.


    Percentage performance error (PE)

    This is the weighted residual of the target value at any given time point. It indicates the deviation of observed value from its predicted value [11]. Mathematically, for the i-th subject, the PE at j-th time point is given by


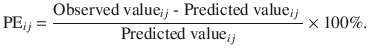
    $$ {\mathrm{PE}}_{ij} = \frac{\mathrm{Observed}\ {\mathrm{value}}_{ij}\ \hbox{-}\ \mathrm{Predicted}\ {\mathrm{value}}_{ij}\ }{{\mathrm{Predicted}\ \mathrm{value}}_{ij}}\times 100\%. $$

     

  2. 2.


    Median performance error (MDPE)

    This is a measure of bias and indicates whether drug delivery with the TCI system is systematically above or below the target value.


    $$ {\mathrm{MDPE}}_i = \mathrm{Median}\ \left\{{\mathrm{PE}}_{i j},\ j=1,\dots, {N}_i\right\} $$
    where N i is the number of observations obtained in the i-th patient.

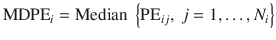
    Alternatively, bias can be expressed as the ratio between observed and predicted values. Logarithmic transformation of the ratio is commonly presented.

     

  3. 3.


    Median absolute performance error (MDAPE)

    This measure indicates the inaccuracy of the TCI system and is a quantitative measure of how far the observed value deviates from the target:


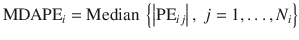
    $$ {\mathrm{MDAPE}}_i = \mathrm{Median}\ \left\{\left|{\mathrm{PE}}_{i j}\right|,\ j=1,\dots, {N}_i\right\} $$

     

  4. 4.


    Wobble

    This index indicates the within-subject variability of the TCI system and is calculated as the median absolute deviation of PE from the bias of the system (MDPE):


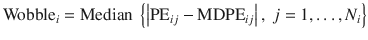
    $$ {\mathrm{Wobble}}_i = \mathrm{Median}\ \left\{\left|{\mathrm{PE}}_{i j}-{\mathrm{MDPE}}_{i j}\right|,\ j=1,\dots, {N}_i\right\} $$

     

  5. 5.


    Divergence

    This is the slope of linear regression between the MDAPE i and time. Divergence shows whether inaccuracy of the TCI system changes over time.

     

An ideal TCI system would produce an observation that matches perfectly with the predicted value. Therefore, the performance error (MDAPE) and bias (MDPE) should approach zero, and the ratio between the observed and predicted value would be of unity. The TCI system should also be stable over time, so that wobble and divergence should be as low as possible.

A useful way to display the performance of a TCI system is to plot the observed and predicted target values over time. Figure 9.2a shows the typical deviations of observed propofol concentration from its predicted value in a patient who was enrolled in a randomized trial evaluating the effect of hyperventilation in patients having craniotomy for removal of brain tumor [12]. Anesthesia was induced and maintained with effect-site-targeted propofol infusion using an open TCI system—computer control infusion pump [13] (CCIP), based on the Schnider pharmacokinetic and pharmacodynamic datasets [14, 15]. Since effect-site concentration cannot be measured, comparisons were made between observed and predicted propofol concentrations in the plasma. Figures 9.2b, c illustrates the bias of the TCI system over time in the same patient. The TCI system produced a lower plasma concentration than predicted during the initial 2 h of infusion. This negative performance error was however offset by the overshoots in the remaining period of anesthesia when the observed plasma concentrations were 14–29 % higher than that of predicted. Consequently, the overall mean ratio of observed-to-predicted concentration (0.99) and MDPE (1.2 %) were small. Inaccuracy (MDAPE) of the TCI system in the patient was 13.8 (95 % confidence intervals (CI): 1.2–27.2 %), Fig. 9.2d.

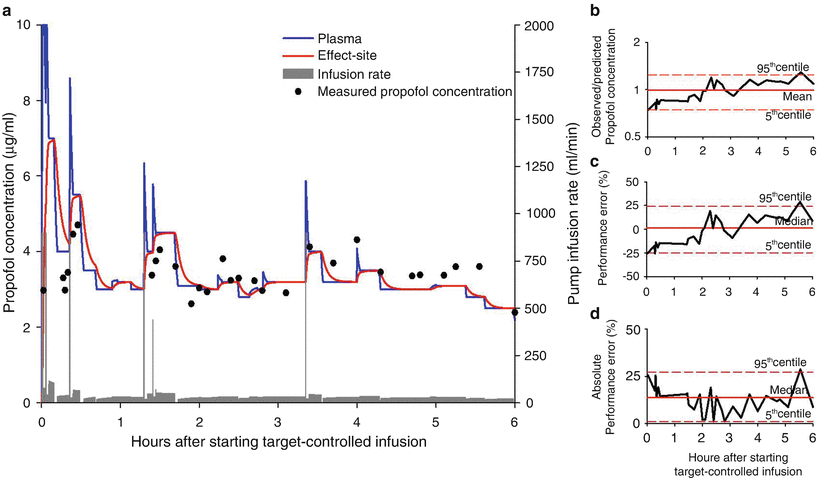
A339434_1_En_9_Fig2_HTML.gif


Fig. 9.2
(a) Target-controlled propofol infusion delivered to a 62-year-old man undergoing excision of frontal tumor. The blue and red lines indicate predicted plasma and effect-site concentrations, respectively. The gray bar shows the pump infusion rate. Measured (observed) propofol concentrations are shown by black circles. (b) Time course of observed-to-predicted propofol concentrations, (c) performance errors, and (d) absolute performance errors. Median (or mean as indicated), 5th, and 95th centile values are also shown

Analyses can also be performed with population data. Figure 9.3 shows the changes of performance error, absolute performance error, and ratio of observed-to-predicted concentrations over time in 30 patients enrolled in our craniotomy hyperventilation trial [12]. By pooling data from all patients, the MDPE was −2.6 % (95% CI: −25.7 to 24.8 %), Fig. 9.3a, and the mean ratio of observed-to-predicted concentration was 0.97 (95% CI: 0.74–1.25), Fig. 9.3b. It should be noted that confidence intervals were wide, suggesting that a large proportion of performance errors were higher or lower than the average values. The MDAPE indicates the overall inaccuracy of the TCI system and was 16.4 % (95% CI: 1.9–27.0 %) in our dataset, Fig. 9.3c. Interestingly, the absolute performance errors tended to become smaller with time, and this indicated convergence of performance with the TCI system (Fig. 9.3d). Finally, in our sample dataset, the median wobble was 15.0 % (95% CI: 3.8–21.0 %), indicating the variability of performance error in each of the subjects.

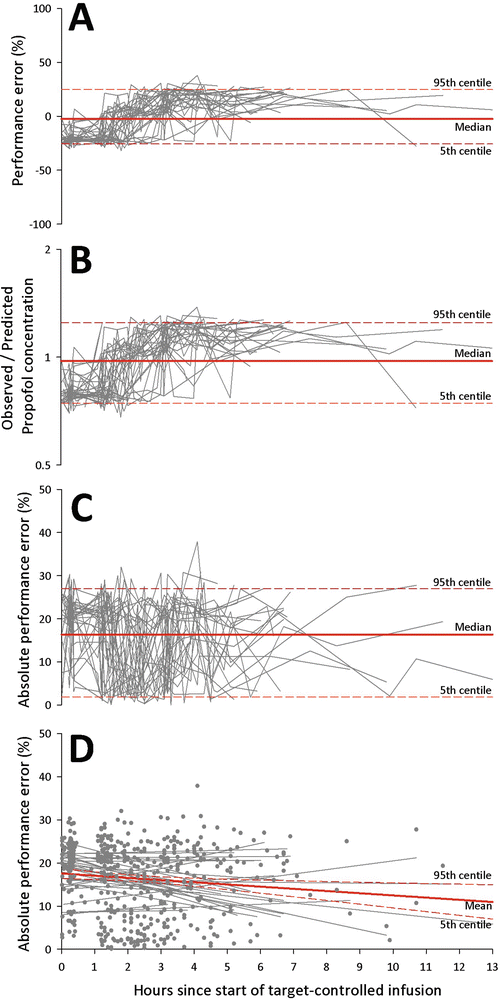
A339434_1_En_9_Fig3_HTML.gif


Fig. 9.3
Time course of (a) performance errors, (b) observed-to-predicted propofol concentrations, (c) absolute performance errors, and (d) regression of absolute performance errors with time in 30 patients having craniotomy for brain tumor excision. Solid line indicates the median (or mean) value. The 5th and 95th centile values are shown as dotted line

These analyses illustrate how the performance indices may be used to quantify the accuracy of TCI system. However, clinical interpretation is more complex. Currently, there is no consensus on the maximum performance error that could be considered acceptable in routine clinical practice. Empirically, Eleveld and colleagues suggested that an absolute performance error <20 % represents good performance, whereas an error >60 % is considered to indicate a poorly performing TCI system [16]. Others have recommended that an absolute performance error <20 to 40 % and a MDPE <10 to 20 % would be clinically acceptable [17, 18]. Although a 20–40 % error seems excessive, this has not been shown to increase the rate of adverse events during TCI [19]. Interestingly, in a systematic study evaluating the discrepancy between end-tidal (predicted) and arterial (observed) isoflurane concentrations, Zbinden and co-workers showed that an ordinary vaporizer produced a negative bias with an arterial isoflurane concentration that was 17.0 % (95% CI: 5.9–27 %) lower than that predicted by end-tidal gas monitoring [20, 21].



Sources of Errors


Table 9.1 summarizes the potential factors that may influence the performance of TCI systems. This includes hardware problems, where inaccuracy of infusion devices may result in a failure to deliver the exact amount of drug intended. In practice, though, hardware problems are rare, and regulatory approval requires that pumps actually administer the intended concentration with high precision. If inaccuracies arise from mechanical problems, then they are more likely to be caused by mechanical failure of one or more components, including problems with the syringe and/or plunger [22–27]. There are also potential software errors, such as incorrect implementation of models or infusion algorithms that might produce large errors in the prediction of drug infusion rates required, or programming errors that might shut down the system unexpectedly. Again, with stringent testing, software errors are rare. Finally, and probably most importantly, there are human errors in drug delivery. This could be due to incorrect pump programming, syringe swap [28], disconnection of venous cannula, or incorrect drug dilution.


Table 9.1
Sources of errors in drug delivery during target-controlled infusion



























Hardware

• Delayed communication or disconnection between the infusion pump and computer

• Inaccuracy of the infusion pump

• Syringe, venous infusion line disconnection

Software

• Inappropriate pharmacokinetic and pharmacodynamic models

• Incorrect infusion rate control algorithms

Human errors

• Syringe swap

• Incorrect drug dilution

• Venous cannula disconnection


Hardware


Before the mid-1990s, limitations in processing power limited technological developments. However, with the advances of computing technology, smaller and faster microprocessors have been developed and incorporated into ordinary syringe pumps to enable implementation of the infusion algorithms required for TCI [29, 30]. Some groups have even developed software programs that are capable of driving syringe pumps from mobile devices through wireless networks without observable delay [31].

Downstream drug delivery could however affect TCI performance. It should be noted that modern syringe pumps are infusion control devices that are capable of delivering a wide range of flow rates from 0.1 to >1000 ml/h. In general, these devices produce an inaccuracy of <±5 % of expected volume infused [32, 33]. Nevertheless, several factors may delay infusion start-up and affect flow stability (Table 9.2). In this respect, a misplaced or loose plunger of a large syringe can delay the onset of infusion [34–39]. This is particularly important when a compliant syringe plunger stopper is used or when compliant infusion delivery lines [40, 41] and antisiphon or anti-reflux devices are used [42–44]. This may contribute to a lower amount of drug being delivered than programmed, resulting in a negative performance error, particularly during the early phase of an infusion. Other factors such as concurrent infusions using multi-access devices [45, 46] and small air bubbles in the infusion line will also contribute to flow irregularity and affect infusion accuracy [47, 48]. There are also extreme conditions, such as strong magnetic fields [49], radio frequency, and hyperbaric conditions [50, 51], that may affect pump performance to different extents. Nevertheless, when hardware problems are carefully prevented by priming of the infusion system (with the flush or purge function) before starting the infusion, the performance error for remifentanil TCI was reduced by 1.6–7.9 % during induction of anesthesia and 0–0.3 % in the maintenance phase [36]. The current data suggest that hardware factors do not contribute substantially to the inaccuracy of TCI systems.


Table 9.2
Factors contributing to drug delivery error in target-controlled infusion




















Factors
Potential mechanisms
Counter measures

Start-up delay
• Loose fitting of syringe plunger

• Large dead space volume in the infusion delivery line

• Large compliant syringe

• Use of antisiphon or anti-reflux devices
• Priming of infusion devices

• Use syringe with smaller diameter

• Tight fit between thumb rest and syringe drive

Flow stability
• Concurrent use of multi-access infusion devices

• Use of antisiphon or anti-reflux devices

• Air bubbles in the infusion delivery line
• Use of dedicated venous line

• Eliminate bubbles in the infusion delivery line


Software


In contrast to hardware performance, the accuracy of TCI is heavily influenced by software factors. In this respect, the prediction performance of TCI systems is heavily dependent on the validity and relevance of the pharmacokinetic model chosen by the user to the patient receiving the infusion. Table 9.3 shows seven sets of pharmacokinetic models for propofol that have been implemented in commercially available and open TCI systems (open systems provide the user with a choice of drugs and models, as opposed to the first generation of pumps, which only enabled TCI of propofol using the Marsh model) [14, 52–60]. It should be noted that the rate constants differ significantly among the different models. Consequently, there is a large variation in the predicted plasma propofol concentration with any given amount of drug infused according to the specific models applied, or conversely that for a given target concentration, the infusion rates necessary, as estimated by the models, will differ significantly. Using computer simulations, Absalom and co-workers found that the Marsh model required at least 20 % more propofol to maintain the same target plasma concentration compared with the Schnider model in middle-aged adults of normal proportions [1]. This finding highlights the importance for specification of appropriate pharmacokinetic model.


Table 9.3
Reported propofol pharmacokinetic models for target-controlled infusion























































































































 
V 1

V 2

V 3

k 10 (min−1)
k 12 (min−1)
k 13 (min−1)
k 14 (min−1)
k 21 (min−1)
k 31 (min−1)
k e0 (min−1)

Dyck [52]
9.64 − (0.051 × age), L/kg
–
571 − (1.66 × age)
(0.652 + 0.015 × weight)/V 1

1.68/V 1

(2.670 − 0.015 × age)/V 1

–
V 1 × k 12/19.4
V 1 × k 13/(571 − 1.66 × age)
–

Gepts [53]
0.228, L/kg
0.476, L/kg
2.895, L/kg
0.119
0.114
0.042
0.00002
0.055
0.003
0.239

Kataria [54]
0.41, L/kg
0.78 × weight + 3.1 × age − 16, L
6.9, L/kg
0.085
k 21 × V 2/V 1

0.063
–
0.077 × weight/(0.78 × weight + 3.1 × age − 16)
0.004
–

Marsh [55]
0.227, L/kg
0.463, L/kg
2.886, L/kg
0.119
0.112
0.042
0.00002
0.055
0.003
0.26

Paedfusor [56–59]
0.458, L/Kg
0.95, L/Kg
5.82, L/Kg
(70 × weight−0.3)/458.3
0.114
0.042
0.00002
0.055
0.003
0.26

Schnider [14]
4.27, L
18.9 − 0.391 × (age, 53), L
238
C 1/V 1

k 21 × V 2/V 1

k31 × V 3/V 1

k 41/10,000
C 2/V 2

C 3/V 3

0.456
     
where

C 1 = 1.89 + [(weight − 77) × 0.046] + [(LBM − 59) × (−0.068)] + [(height − 177) × 0.026]

C 2 = 1.29 − 0.024 × (age − 53)

C 3 = 0.836

LBM = 1.1 × weight − 128 × (weight/height)2 for male

or 1.07 × weight − 148 × (weight/height)2 for female
    

Tackley [60]
0.32, L/kg
0.525, L/kg
2.071, L/kg
0.087
0.105
0.022
–
0.064
0.003
–


LBM lean body mass


Performance of Target-Controlled Infusions


In order to select the best pharmacokinetic model, one needs to understand the underlying processes in deriving these datasets. Table 9.4 summarizes the patient characteristics of studies producing the various pharmacokinetic models for opioids [61–72], etomidate [73], ketamine [74], midazolam [75], thiopental [76, 77], propofol [14, 16, 52 –60, 78, 79], and muscle relaxants [80]. Earlier studies recruited a small number of volunteers or healthy patients having trivial elective surgery, and their pharmacokinetic parameters may not represent those patients at extreme age with multiple comorbidities. There are also important differences in the study methodology, such as the use of venous sampling in the Marsh model [55] which might have underestimated the plasma propofol concentration, because venous sampling produced lower concentrations than arterial measurements.


Table 9.4
Patient characteristics of commonly used pharmacokinetic dataset in target-controlled infusion



















































































































































AuthorReference

Patient characteristics
No. of patients
Male sex, no. (%)
Covariates

Alfentanil

Lemmens [61]
Adults (24–79 years), ASA 1–2
36
15 (41.7)
Weight (≤50 vs. >50 years), gender

Maitre [62]
Adults with various risks (24–91 years), ASA 1–3
45
–
Weight, age, gender

Scott [63]
Adults (20–89 years), ASA 1–2
17
17 (100)
Weight

Fentanyl

Hudson [64]
Adults (67.2 ± 8.7 years)b, ASA 2–3
10
9 (90)
Weight

McClain [65]
Healthy volunteers (22–29 years)
7
7 (100)
Weight

Scott [63]
Adults (20–89 years), ASA 1–2
17
17 (100)
Weight

Shafer [66]
Adults (58 ± 11 years)b, ASA 1–4
21
7 (33.3)
Weight

Varvel [67]
Adults (33–57 years), ASA 1–2
8
3 (37.5)
Weight

Remifentanil

Egan [68]
Healthy volunteers (22–38 years)
10
10 (100)
Weight

Minto [69, 70]
Healthy volunteers (60–65 years)
65
38 (58.5)
Age, gender, lean body mass (weight and height)

Sufentanil

Bovill [71]
Adults (22–64 years), ASA 1–2
10
7 (70)
Weight

Gepts [72]
Adults (14–68 years), ASA 1–2
25
14 (56)
Weight

Etomidate

Arden [73]
Adults (22–82 years), ASA 1–2
21
20 (95.2)
Weight

Ketamine

Domino [74]
Healthy volunteers (26–41 years)
8
8 (100)
Weight

Midazolam

Greenblatt [75]
Healthy volunteers (24–37 years)
20
10 (50)
Weight

Elderly volunteers (60–79 years)
20
9 (45)
Weight

Propofol

Dyck [52]
Adults (20 ≥ 65 years)
60
60 (100)
Weight, age

Eleveld [16]
Patients/volunteers from 21 datasets (0–88 years)
660
433 (72.2)
Weight, age, gender, healthy (vs. patient)

Gepts [53]
Adults, ASA 1
18
13 (72.2)
Weight

Kataria [54]

Only gold members can continue reading. Log In or Register to continue

Related posts:

Default ThumbnailClinical Effects and Applications of Ketamine Sedation of the Critically Ill Child Clinical Pharmacology of Intravenous Sedation in Children Dexmedetomidine: The Science and Clinical Aspects in Adults and Children EEG Monitoring of Depth of Anesthesia TCI/TIVA Adult Case Studies
Tags:
Jul 14, 2017 | Posted by in Uncategorized | Comments Off on Performance of Target-Controlled Infusion Systems

Full access? Get Clinical Tree

 Get Clinical Tree app for offline access