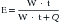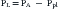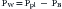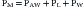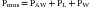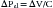Chapter 42 Mechanical Dysfunction of the Respiratory System
Work, Power, and Energy Expenditure in the Respiratory System
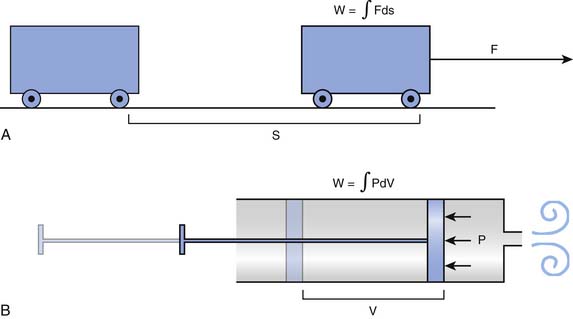
In simple intuitive terms, the variable that best sums up the function of a muscle-powered pump is the mechanical load that the contraction of the powering muscles must overcome with each pump cycle. Over time, mechanical load translates into power (the product of work by the time that it takes to carry it out) and energy expenditure. Accordingly, whether the respiratory muscles can carry a given mechanical load is ultimately determined by their ability to generate work from the limited amount of energy that they receive from their blood supply. The first law of thermodynamics stipulates that when a certain amount of energy is added to a closed system by an external source (in this case the metabolism of fuels supplied by the circulation to the respiratory muscles), the resultant change in the system’s internal energy may either be applied to perform external work (W) over a period of time (t) or is dissipated as heat (Q). Implicit in this statement is the fact that only a portion of the energy that the respiratory muscles derive from metabolic substrates is transformed into respiratory work. This proportion varies depending on the system’s efficiency (E), defined as:
Determinants of Respiratory Work
Every high school physics student learns to calculate the external work done to move an object between two points as the product of the force needed to overcome all resistances to the movement by the distance between the points. Because the force may change along the way, the same student may learn at some point that it is more precise to break the movement into many elementary components and then add up all the work components by integration, as shown in Figure 42-1, A.
The mathematical subtleties of this distinction may become a little clearer if we compare the breath to the action of a syringe, where, by pushing or pulling on the plunger, we create a pressure (P), positive or negative, that has the effect of changing the volume contained in the barrel (V). The work done in this process can be determined by integrating the product P · dV, as shown in Figure 42-1, B. The obvious corollary is that the work done by the respiratory muscles and, by extension, the energy that must be supplied to these muscles are both defined by the volume-pressure relationships of the lungs and the chest wall.
Volume-Pressure Relationships
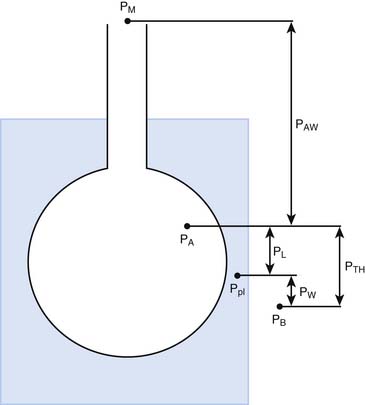
The pressures needed to inflate the thorax, the lungs, and the chest wall are, however, different from each other. Respiratory physiologists have traditionally approached the analysis of these pressures by taking an imaginary walk from the mouth down the airways to the alveolus, across the lung tissue and visceral pleura to the pleural space, and finally across the chest wall to the surface of the chest (Figure 42-2). The difference between the pressures measured at two consecutive stops is the driving pressure needed to cause or maintain a certain volume displacement:
Consider first a situation in which the lungs undergo passive distention, without participation of the respiratory muscles. This is what happens during positive airway pressure ventilation, when the pressure drive for inflation of the thorax is provided by PM. By performing a series of substitutions in equations 3through 5 and assuming PB = 0, we can easily arrive to the following equality:
which reveals that, from a mechanical point of view, the components of the respiratory system form a series arrangement, whereby the total pressure needed to generate a movement is the sum of the pressures generated in the airways, the lungs, and the chest wall. Respiratory physiologists have often borrowed from electrical theory, assuming, perhaps to the dismay of many readers, that the black and white simplicity of electrical circuitry is less intimidating than the complexities of Newtonian mechanics. When speaking of electrical circuits, the term series indicates that every element in the circuit experiences the same current as the circuit as a whole, but the total voltage across the circuit is the sum of the voltages across the individual elements. Because current is the electrical analog of flow (volume per unit of time) and voltage is the analog of pressure, it is easy to see how Equations 2 and 6 justify the overall electrical analogy, even though many readers may be less impressed by how much conceptual clarity it sheds for them.
The mechanical behavior of the airways and the lungs does not change substantially during muscle-powered breathing. The behavior of the chest wall, on the other hand, is greatly influenced by the contraction of the respiratory muscles. Because the muscles not only act on the wall but are also part of the wall itself, any attempt to define mathematically the behavior of the chest wall during a spontaneous breath becomes a futile exercise. For our purposes here, however, it may suffice to say that, during spontaneous breathing, equation 6 can be modified as:
where Pmus represents the pressure generated by the muscles’ contraction, inclusive of the effects that this contraction has on the behavior of the chest wall itself. Thus every time we take a breath, the neural output to the respiratory muscles is adjusted to overcome as precisely as possible the opposing pressures generated by the respiratory system.
Nature of the Mechanical Forces Acting on the Respiratory Pump
Disease induces alterations in these physical processes and therefore also in the forces and pressures that result from them. To relate these alterations to the disease’s clinical manifestations, it is helpful to classify both processes and pressures into nondissipative and dissipative, depending on whether the energy consumed stays in or leaves the system. For instance, elasticity is typically a nondissipative process because the energy needed to produce elastic deformation during inspiration is accumulated in the tissues and then used to empty the lungs during expiration. In contrast, all resistive processes are dissipative: the energy liberated by the friction of the gas against the airway walls or by the molecular interactions within the tissue is transformed into heat and transported outside of the system by the blood or the expired gas.
Nondissipative Phenomena: Elastic Behavior of the Respiratory System
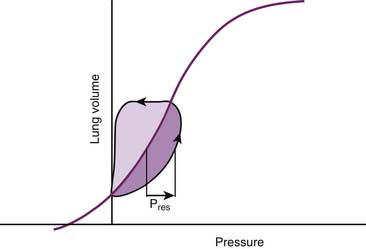
By obtaining measurements at various volumes and then plotting volume against PA, PL, and PW, we can compare the volume-pressure relationships of the thorax as a whole with those of the lungs and the chest wall. Not unexpectedly given the heterogeneous composition of the structures involved, the relationships are complex and cannot be described in a simple mathematical equation (Figure 42-3). In all three cases, the plotted curve has a sigmoidlike shape, with pressure increasing rapidly relative to volume at low and high volumes and more slowly at middle volumes.1
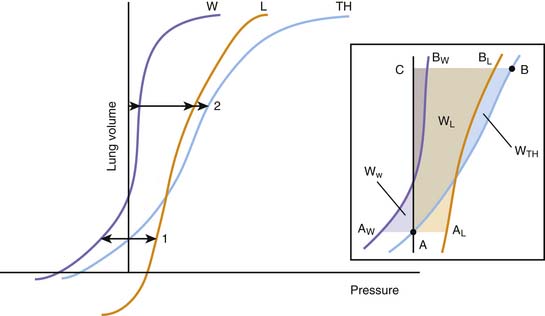
Figure 42–3 Idealized representation of the static volume-pressure relationships of the thorax (TH), lungs (L), and chest wall (W). Pressure, on the abscissa, represents the pressure across the thorax as a whole (PTH = PA – PB), lungs (PL = PA – PL), and chest wall (PW = Ppl – PB; see Figure 42-2). The arrows indicate the magnitude and direction of the pressures acting on the thorax and its components at two volumes: (1) the relaxation volume of the thorax, where the recoils of the lung and the chest wall neutralize each other; and (2) an arbitrary volume where the recoils of the lungs and the chest wall act both in the direction of reducing thoracic volume. Inset: Detail of the same curves, indicating the elastic work done on the thorax as a whole and each of its components for a volume displacement starting at a volume A (the relaxation volume of the thorax) and ending at a volume C. The work done on the thorax as a whole is represented by the area A-B-C; the work done on the lungs by A-AL-BL-C; and the work done on the chest wall by AW-A-BW-C. A portion of the work done on the chest wall (the triangular area in purple between AW and the ordinate axis) is contributed by the recoil of the chest wall, which between those points facilitates the action of the respiratory muscles.
Being a continuous function, each volume-pressure relationship has a defined slope at any given volume (dV/dP). This slope defines the compliance of the thorax, lungs, or chest wall for that particular volume, depending on whether dP is replaced by dPA, dPL, or dPW. Although a cursory examination of Figure 42-3 reveals that both the lung and chest wall compliances defined in this manner vary markedly over the entire range of volumes, on closer inspection, the ratio dV/dP is relatively constant at normal breathing volumes. Thus for these volumes, it is safe to write:
where ΔPel represents the change in elastic recoil pressure of the thorax (ΔPA), lungs (ΔPL), or chest wall (ΔPW) for a lung volume excursion ΔV, and C is the compliance of the corresponding component. As lung volume decreases or increases beyond this linear range, dV/dP starts to decrease in a volume-dependent manner, and the respiratory muscles must generate progressively larger pressures to produce the same volume change. Disease frequently causes the lungs to operate outside of their linear volume-pressure range, thereby increasing both the work of breathing and the energy needed to do it.
At any given volume, the lungs, the chest wall, and the thorax each generate a certain elastic pressure or recoil. This recoil can act to increase or decrease volume (as indicated by the direction of the arrows in Figure 42-4). By definition, elastic recoil drives the thorax and its individual components to adopt a volume, known as the relaxation volume, at which recoil itself is extinguished. The relaxation volumes of the lungs and the chest wall are the volumes that each of these components would adopt if all the mechanical constraints imposed by their mutual attachments and interactions were removed. The relaxation volume of the thorax, in contrast, is defined by the mechanical interaction of the lungs and the chest wall. It coincides with the point at which the opposing elastic recoils of these two components neutralize each other (as shown by the equal magnitude but opposite pressure vectors in Figure 42-4).
In the adult, the relaxation volume of the lungs is lower than the residual volume (the volume of gas contained in the lungs at the end of a forced expiration). The relaxation volume of the chest wall, by contrast, exceeds 50% of the vital capacity (the maximal volume of gas that can be inhaled from residual volume). This discrepancy in the relaxation volumes of the lungs and chest wall has three important consequences. First, it forces the relaxation volume of the thorax as a whole to occupy a position intermediate between the relaxation volumes of the lungs and the chest wall (at approximately 35% of vital capacity). Under most circumstances, this volume coincides with the functional residual capacity (FRC), which is the volume contained in the lungs at the end of a tidal expiration. Second, as the thorax starts to rise above its relaxation volume during inspiration, the outward recoil of the chest wall contributes to the expansion of the lungs, thereby reducing the work that the respiratory muscles need to perform during normal breathing (see Figure 42-3, inset, where the work done by the chest wall at the beginning of a breath is represented by WW). Finally, at normal breathing volumes, the opposing actions of the lungs and chest wall recoils create a negative pressure at the boundaries of the lung tissue with the chest wall and the other intrathoracic structures. This negative pressure is an important contributor to the return of venous blood to the chest. The static volume-pressure relationships of the lungs and chest wall vary depending on their state of maturation and health (see Figure 42-4). In the infant, the chest wall generates remarkably little outward recoil within the normal range of breathing volumes.2–5 Because the inward recoil of the lungs varies little with respect to lung size and age during development,6–8 the relaxation volume of the infant’s thorax is proportionally smaller than that of the adult (as shown in Figure 42-4 by the lower intercept of the volume-pressure relationship of the thorax and the ordinate axis). If, as occurs in the adult, the FRC coincided with this relaxation volume (15% of vital capacity compared with 35% in the adult), then the infant would be at a definite disadvantage in terms of alveolar stability and oxygenation. The newborns of most mammalian species, however, have developed physiologic strategies to maintain their FRC above the relaxation volume of the thorax.9 These strategies are generally directed at interrupting expiratory flow before expiration is complete and include shortening of the expiratory time,10 contraction of adductor muscles of the glottis to retard exhalation,11,12 and persistence of the tonic activity of the inspiratory muscles during expiration.13 Being so dependent on the pattern of breathing, the FRC of the newborn and small infant is very vulnerable to changes in muscle coordination and tone. As an example, the decrease of tonic activity of the respiratory and laryngeal muscles associated with rapid eye movement sleep13 may cause a substantial reduction in thoracic lung volume at these ages. Similarly, muscle weakness, anesthesia, deep sedation, and central nervous system depression in general tend to lower FRC below levels compatible with alveolar stability. Under such circumstances, alveoli close, and both the shunt fraction and the work of breathing increase.
Lungs/Chest Wall Interactions
Although, considered in isolation, the lungs and the chest wall have different volume-pressure relationships, their mechanical linkage at the pleural space prevents them from changing volume independently. By sharing a common boundary, the lungs and chest wall are also influenced simultaneously by variations in the pressure at this boundary. The resultant interplay is well illustrated by the effects of a pneumothorax, a complication that is quite familiar to readers who practice intensive care medicine. When a certain volume of air enters the pleural space, the most immediate effect is an increase in the pleural pressure (ΔP). This increase causes the effective transmural pressures of the lungs and chest wall to change by the same absolute amount, but in opposite direction: transpulmonary pressure (PA − Ppl) decreases by -ΔP, whereas chest wall transmural pressure (Ppl) increases by ΔP. No longer held together by a rigid boundary, the lungs and the chest wall respond to the change in transmural pressure by decreasing and increasing volume along their respective volume-pressure relationships (Figure 42-5). Consequently, one could say that the volume of air originally introduced in the pleural cavity is partitioned into two components, one the volume by which the lungs collapse and the other the volume by which the chest wall expands. The relative sizes of the lung collapse and the chest wall expansion are dictated by the volume-pressure relationships of the lungs and chest wall. If the compliance of the chest wall exceeds the compliance of the lungs (as is usually the case in the infant), then the chest wall expands more than the lungs collapse. The difference is even greater when lung compliance is reduced by disease (Figure 42-5, B). Then the chest wall absorbs the majority of the volume change while the lungs barely decrease their volume. This simple analysis explains why noncompliant lungs show surprisingly little collapse when a pneumothorax develops, a finding that is often mistakenly attributed to the “stiffness” of the lung parenchyma. It also provides an opportunity to point out that the magnitude of the chest wall expansion, although frequently overlooked in radiographs, relates more directly to the true malignancy of a pneumothorax (compression of vascular structures) than does the usually more apparent collapse of the lungs.
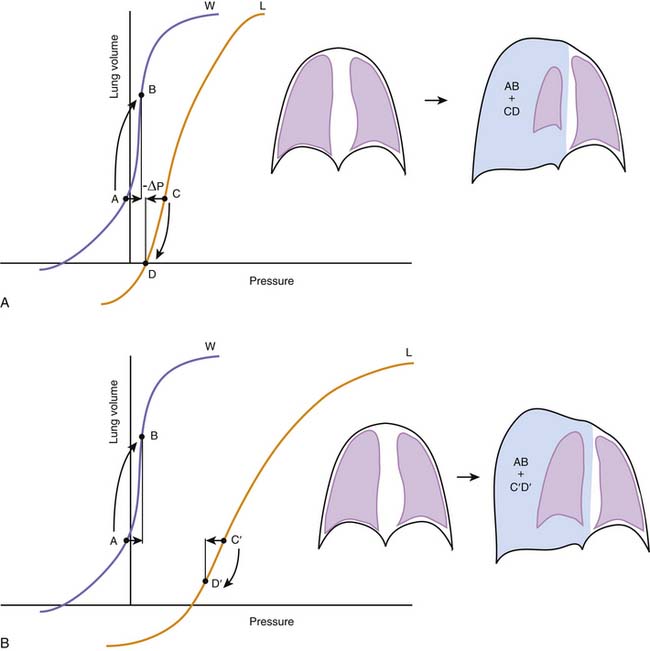
Figure 42–5 A, The effects of a pneumothorax are used here to illustrate the interdependence between the elastic recoils of the lungs and the chest wall. Pressures, on the abscissa, represent the transmural pressures of the lungs (L, PA – Ppl, see Figures 42-2 and 42-3) and chest wall (W, Ppl – PB). The introduction of a volume of gas into the pleural space raises pleural pressure by a magnitude ΔP, which changes both transmural pressures by the same absolute magnitude, but in opposite directions. Lungs and chest wall respond to the change in transmural pressure by decreasing (C→D) and increasing their volume (A→B) along their respective volume-pressure relationships. The volume of the pneumothorax is thus partitioned between the lungs and the chest wall according to their relative compliances. B, When lung compliance is decreased by disease, the volume pressure relationship of the lungs is displaced to the right and has a lower slope. Under these circumstances, the chest wall is forced to accommodate the majority of the volume change introduced by the pneumothorax (AB >> C’D’), giving perhaps the wrong impression that the stiffness of the lungs prevents them from collapsing further.
Dissipative Forces
Dynamic Volume-Pressure Relationships
Analysis of the volume-pressure relationships of the thorax and its components becomes more complicated when we consider the pressure changes generated by gas flow and by the movement of the lung and chest wall tissue as the lungs inflate and deflate. These pressure changes result from molecular interactions between the gas and the airway walls, within the gas stream itself, and among the components of the gas-liquid interface and the tissue. The same interactions are responsible for well-known physical phenomena such as viscosity (the internal resistance of a fluid to flow), turbulence (the development of chaotic movements within a flowing fluid), or viscoelasticity (a property of tissues and fluids that causes their deformations to be time-dependent rather than instantaneous; ketchup provides a good example when it hangs stubbornly to the bottle before being released after multiple taps).14–17
Regardless of their ultimate physical nature, all the phenomena that occupy our attention at this point have two characteristics in common. The first is that they always result in a net loss or dissipation of energy from the respiratory system. The lost energy can no longer be used to perform work, and consequently dissipative pressure losses cause the volume-pressure relationships of the respiratory system to follow a different trajectory depending on the direction of the volume change. This property, known as hysteresis, is responsible for the development of loops when the volume-pressure relationships are plotted continuously during a breath (Figure 42-6). In this graphic representation, the dissipative pressures can be easily identified as the horizontal distance between the volume-pressure tracing and the corresponding point on the elastic volume-pressure relationship. The work done against these pressures can be quantified as the area enclosed by the loop.
< div class='tao-gold-member'>

Full access? Get Clinical Tree