Adjusted body weight (kg) [28]: Was derived to scale doses in the obese. It uses the ideal weight (IBW) and to a varying degree the amount of weight excess (TBW-IBW), which must be adjusted by a correcting factor (CF) based on the physical properties of the drug. In anesthesia it has been used to scale doses of propofol using a CF of 0.4 with good results [29, 30]. Its calculation is simple, and requires the weight, height, and gender of the patient.
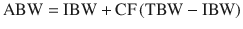
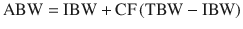
Lean body weight (LBW): Is the difference between total body weight (TBW) and fat mass. Normally lean mass is between 70 % and 90 % of TBW. This ratio is altered in obesity due to excess fat. This descriptor has been recommended to adjust different doses of drugs in obese patients and non-obese [27]. Lean mass has a better correlation with metabolic processes than TBW, due to the lower contribution of fat to metabolic activity [27]. There are various formulas for calculating the lean mass, the most commonly used being those of James [31], and Hume [32]. Their calculation requires the weight, height, and gender of the patient.
James equation:
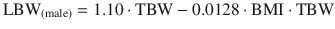
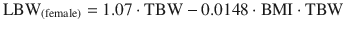where the body mass index (BMI) is calculated as:
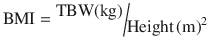
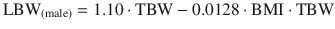
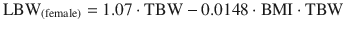
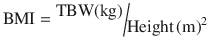
Hume equation:
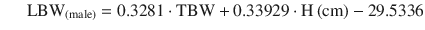
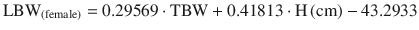
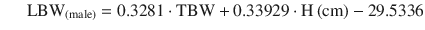
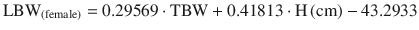
Using the James equation progressive weight gain entails an increase in lean mass until a BMI limit of 35 women and 42 men is reached. From then on the estimate of LBM starts to decrease until eventually reaching negative values, and so is inadequate in the morbidly obese (Fig. 24.1). Pharmacokinetic models such as the Schnider for propofol [33] and the Minto for Remifentanil [34] use this equation to calculate LBM as a covariate in some of its parameters, creating problems in the morbidly obese as discussed below.
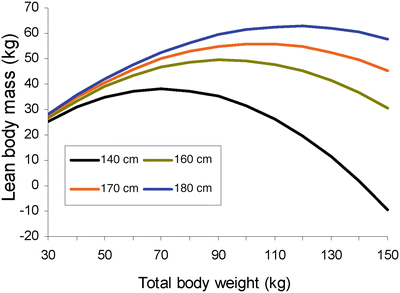
Fig. 24.1
Relationship between total body weight and lean body mass (LBM) of women according to James’ equation for patients of different height
Fat-free mass (FFM)
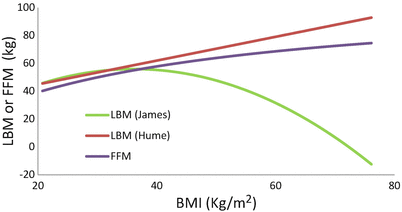
Fat-free mass (FFM) [2] considers muscles, bones, vital organs, and extracellular fluid. Unlike lean mass, it excludes lipid cell membranes, bone, and the central nervous system. Therefore FFM is very similar to lean mass and its main advantage is that it was derived from unbiased body mass measurements in people of a wide range of body weight (40–216 kg). The formula can be applied to the morbidly obese without the problems seen with the James equation (Fig. 24.2). FFM is determined using the weight (kg), height (m), and gender of the patient.
![$$ \mathrm{F}\mathrm{F}\mathrm{M}={\mathrm{WHS}}_{\max}\cdot {\mathrm{H}}^2\cdot \left[\raisebox{1ex}{$\mathrm{TBW}$}\!\left/ \!\raisebox{-1ex}{$\left({\mathrm{WHS}}_{50}\cdot {\mathrm{H}}^2+\mathrm{T}\mathrm{B}\mathrm{W}\right)$}\right.\right] $$](/wp-content/uploads/2017/07/A339434_1_En_24_Chapter_Equh.gif)
For men, WHSmax is 42.92 kg/m2 and WHS50 is 30.93 kg/m2 and for women WHSmax is 37.99 kg/m2 and WHS50 is 35.98 kg/m2.
Fig. 24.2
Relationship between BMI and lean body mass (LBM) of women estimated by James and Hume equations and FFM (Janmahasatian Equation)
Normal fat mass (NFM)
NFM is an extension of the concept of ABW and predicted normal weight [34]. It incorporates an estimate of FFM plus a variable percentage (FFAT) of the estimated fat mass (TBW-FFM).
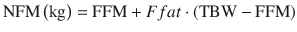The idea of NFM is to determine the value of Ffat that is most appropriate for the parameter being predicted. This will depend on the physical properties of the drug. If Ffat is estimated to be zero, then FFM alone is required to predict size while if Ffat is 1 then size is predicted by TBW.
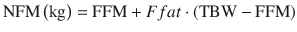
Linear Body Weight Dosage Models
The larger body size of obese patients commonly causes a greater drug distribution volume and clearance. The magnitude of this rise is, however, variable depending on the characteristics of each drug [35]. Linear per kg dosing models assume that volumes and clearances increase proportionally to body weight. Commonly, pharmacokinetic models derived from normal weight patients use linear relationships between weight and model parameters [36– 38]. Using these models in obese patients puts them at risk of overdose, mainly because the clearance of a drug does not increase linearly with weight [39]. The use of other size descriptors to scale down clearances, such as lean mass or normal fat mass (NFM), allows a better description of this nonlinear relationship [27]. In turn, allometric scaling models have been successfully used to describe changes in volumes and clearances of patients within a wide range of weight , as described below [17, 18, 40–42].
Allometry
Different organisms’ characteristics and bodily functions can be scaled to body size by an exponential relationship to the power of a multiple of 1/4 [43]. Allometry describes this exponential relationship between size and function.
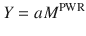where Y is the predicted biological characteristic, M is the mass of the body, a is an empirically derived constant, and PWR is the allometric exponent.
The growth of living beings, from single cell organisms to obese humans and elephants, can be described using allometric relationships. It is known, for example, that as living beings grow they do not remain isometric (same shape) because they would not be able to support their own weight—thus resulting in disproportional changes in body structure and composition. Allometry applies to many physiological, structural, and time related variables which follow the ¼ power law [43].
Allometry has been successfully used in pharmacology to adjust doses between different body sizes within species or between different species [44–46]. An allometric model based on theoretical principles scales volumes using a power of 1, clearances using a power of ¾, and half-times with a power of ¼, with respect to body size—no matter which body size descriptor is used, since that will depend on the physical properties of the drug [41, 47]. The basis of using a power of ¾ for clearances comes from its metabolic nature [43, 48]. There is strong evidence throughout a variety of species, including humans, that the basal metabolic rate can be adjusted according to body size using an allometric power of ¾ [43, 49]. Similarly, it is known that the metabolic rate of an organism is proportional to the energy produced by muscles, and can be scaled to body size using a power of ¾. In intravenous anesthesia there are many examples of the appropriateness of allometric relationships to describe the pharmacokinetic changes associated with growth in children [44–46] and obesity related size changes [17, 18, 41, 42, 47].
TIVA and TCI in the Obese Patient
Traditionally the administration of intravenous anesthesia using TCI in the obese has been done using dosing models derived from non-obese patients. The use of such models has proven inadequate in this population [41, 50]. Recently, however, there has been great interest in developing new PK and PD models that include obese patients. In this section we shall attempt to describe the pharmacokinetic changes associated with obesity, applied to frequently used intravenous anesthetics .
Opioids
Opioids are often used in general anesthesia to provide analgesia. Precise dosing in obese patients is crucial due to their greater susceptibility of developing respiratory complications . Nevertheless, the dose of opioids is often guided more by intuition than by scientific evidence. Furthermore, unlike the hypnotics, where there have been great advances in the monitoring of effect using EEG readings, to date there are no means to adequately monitor the effects of intra-operative opioid administration (see Chap. X on monitoring of the analgesic component of anesthesia).
Fentanyl
There are no pharmacokinetic models for fentanyl in the obese. Its pharmacokinetics are usually described using 3-compartment models, emphasizing its high lipid solubility (partition coefficient octanol-H2O = 813), high volume of distribution (262 L), and relatively low clearance (CL = 0.5 L/min) [51]. These features cause long infusions, or repeated boluses of fentanyl to result in accumulation in peripheral tissues, especially fat tissue, potentially prolonging its duration of action [52]. Accumulation of this drug can be expected to increase in the obese due to the excess of fat mass. In turn, the increased cardiac output in these patients should result in increased clearances relative to normal weight patients. Shibutani et al. [53] evaluated the predictive ability of two pharmacokinetic models of fentanyl in obese and normal weight patients. In both models results showed a tendency to overestimate the concentrations of fentanyl in the obese. This is because the pharmacokinetic parameters of the models used were not scaled to weight and therefore were only representative of thin patients. In other words, the models did not consider the expected increase in volumes and clearances in these patients. In the same study, the authors were able to characterize the metabolic clearance and its relationship with weight, finding a nonlinear relationship . Based on their findings they suggest a standardized dose based on an empirical descriptor of body size called “pharmacokinetic mass .”
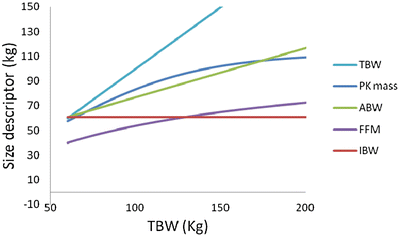
![$$ \begin{array}{l}\mathrm{Pharmacokinetic}\ \mathrm{mass}\\ {}=52/\left[1+\left(196.4{\mathrm{e}}^{-0.025}\times \mathrm{T}\mathrm{B}\mathrm{W}-53.66/100\right)\right]\hfill \end{array} $$](/wp-content/uploads/2017/07/A339434_1_En_24_Chapter_Equk.gif)
Figure 24.3 shows the relationship between weight and different size descriptors including pharmacokinetic mass. This figure suggests that, of the traditional size descriptors, the ABW with a correction factor of 0.4 (similar to that suggested for propofol ) is the closest to the derived descriptor for this drug and could be a simple way of adjusting its dose.
Fig. 24.3
Relationship between weight and different size descriptors including pharmacokinetic mass
Alfentanil
The pharmacokinetics of alfentanil are commonly described using a 3-compartment model [37]. Its pharmacokinetic characteristics include its relatively low lipid solubility (partition coefficient octanol-H2O = 145), a volume of distribution of only 23 L and a slow clearance (CL = 0.2 L/min) [51]. Its lower lipid solubility compared to other opioids should lead to less accumulation in obese patients. There is only one PK model for this drug in obese patients, published by Pérus et al. [38], and this model was based on the study of only ten obese and six non-obese patients. In that study the authors found that the model of Maitre [37], derived from non-obese patients, underestimated alfentanil concentrations in obese patients—which could lead to an overdose. This error in estimation is attributed to the use of a lineal model based on weight to estimate volumes and clearances. Furthermore, based on the modeling analysis the authors describe an increase in alfentanil clearance in the obese, without any apparent effect on other parameters. With the scarce data available on this drug, definite recommendations cannot be made . It seems, however, reasonable to advise dosing of alfentanil using a descriptor of size such as lean mass (FFM) and not body weight.
Sufentanil
The pharmacokinetics of sufentanil are described using 2- and 3-compartment models. Its pharmacokinetic profile emphasizes its high lipid solubility (partition coefficient octanol-H2O = 1778), high volume of distribution (541 L), and a relatively high clearance (CL = 1.2 L/min) [51, 54]. There are two models of sufentanil derived from an obese population [55, 56]. Unfortunately, due to limitations in their designs none of these studies is able to characterize the effect of body size as a continuous variable in volumes and clearances of the drug. Schwartz et al. [55] described the pharmacokinetics of sufentanil in eight obese and eight non-obese patients. The authors used a 2-compartment model to describe sufentanil PK and found a larger volume of distribution in obese (547 L) compared to non-obese (346 L) patients. With regard to clearance, they report slightly higher value of 1.99 (L/min) in obese compared with 1.78 (L/min) in the non-obese, however this difference was not statistically significant. Slepchenko et al. [56] administered sufentanil by TCI in obese subjects using the non-obese model created by Gepts et al. [57]. The authors found an overall good performance, with a slight tendency to overestimate the drug concentration (“Median performance error” = −13 %). Although this result could be interpreted as a validation of this model in the obese, there remains a clear correlation between the degree of obesity and the amount of overestimation. That is, the error becomes more negative (more overestimation) with increasing weight, which could be explained because the model does not scale its parameters according to body size. Therefore, in heavier patients, there is a greater the risk of underdosing, because the model does not consider the expected increase in volumes and clearances of sufentanil as weight increase. Using the pharmacokinetic parameters reported by Schwartz et al. [55] in obese and non-obese patients, it is possible to simulate dosing using different size descriptors (Fig. 24.4). The figure shows that weight-based schemes result in higher concentrations in obese patients, and that dose normalization based on FFM or ABW would be preferable.
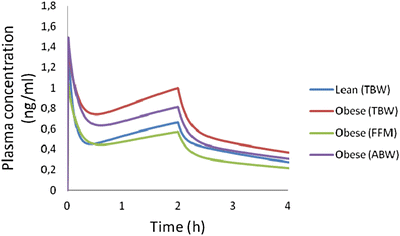
Fig. 24.4
Simulation of plasma concentration of sufentanil in a 70 kg (lean) and a 94 kg (obese) patient, both 170 cm tall. The dose of sufentanil administered is a 4 mcg/kg bolus, followed by a continuous infusion of 0.1 mcg/kg/min for 2 h. Obese patient schemes are based on actual weight (TBW), lean mass (FFM), or adjusted body weight, with a correcting factor of 0.4 (ABW)
Remifentanil
The pharmacokinetics of remifentanil are characterized using 2- or 3-compartment models [14, 34, 58]. Its pharmacokinetic profile includes a moderate lipid solubility (partition coefficient octanol-H2O = 17.9), low volume of distribution (20 L), and a rapid clearance (CL = 2.6 L/min). Egan et al. [14] described the pharmacokinetics of remifentanil after a large single bolus of approximately 10 mcg/kg (TBW) in 12 obese and 12 non-obese patients. In their results, the authors report higher concentrations and a longer duration of associated hemodynamic compromise in obese patients. Using a two-compartment model to describe the pharmacokinetics of the drug, the authors found no differences in volumes (L) and clearances (L/min) in both groups. It should be noted, however, that there was a tendency to a slight increase in volumes and clearances in obese patients, which was better correlated with the increase in lean mass than total body weight . This correlation explains overdose reported in obese patients when using a bolus scaled to weight. The model they designed suggests scaling of doses using lean mass. This is shown in Fig. 24.5 using the parameters reported by Egan et al. and different size descriptors.
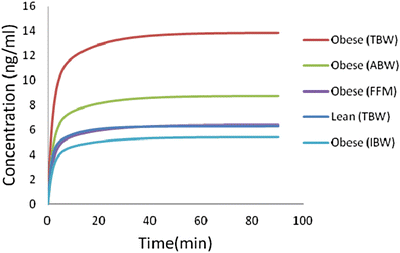
Fig. 24.5
Simulation of plasma concentration of remifentanil using the Egan model, in two patients—one 70 kg (lean) and the other 94 kg (obese), both 170 cm tall. The dose administered of remifentanil is 0.25 mcg/kg/min. Obese patient schemes are based on actual weight (TBW), lean mass (FFM), adjusted body weight, with a correcting factor of 0.4 (ABW) or ideal body weight (IBW)
Remifentanil TCI with the Minto PK Model in the Obese
The administration of remifentanil by TCI using the Minto model [34] is not recommended for the morbidly obese as this model was not derived from obese patients. As mentioned above, the James equation [31], used in this model to calculate lean mass, produces an underestimation of V1, V2, and CL in the morbidly obese (Table 24.1). If this model is used for TCI in patients with a BMI above a critical value (~35 in women and ~42 in men), the amount of drug administered will be progressively less than required. La Colla et al. [59] demonstrated that underestimation with the Minto model in the morbidly obese can be corrected by using the Janmahasatian equation [2], instead of the James equation, for estimating FFM. This correction, nevertheless, has not been incorporated into commercially available TCI pumps. Alternatively, the use of a larger “fake height” to reduce error with the James equation has also been proposed by the same authors [59]. We believe that until there are adequate remifentanil TCI models implemented for use in obese patients, continuous infusions schemes based on FFM and adjusted according to clinical response should be preferred.
Table 24.1
Pharmacokinetic parameters adjusted to LBM (James equation) in the Minto model for remifentanil
Parameter | Non-obese | Obese |
|---|---|---|
V1 (L) | 4.4 | 3.3 |
V1 (L) | 8.8 | 7.2 |
CL (L/h) | 144 | 128 |
Propofol
Propofol is the hypnotic of choice for TIVA. Its pharmacokinetics are best described by three-compartment models [33, 36, 60–64]. Its pharmacokinetic profile features a high lipid solubility (partition coefficient octanol-H2O = 6800), a high volume of distribution (≈250 L), and rapid clearance (≈1.8 L/min). Several studies have examined the pharmacokinetics of propofol in obese patients. Servin et al. [30] designed the first formal pharmacokinetic study of propofol in eight morbidly obese patients. The authors reported that the initial volume of distribution was not modified in obese patients, compared with the non-obese adults using data from another study. Furthermore, clearance and distribution volume at steady state were correlated to TBW. The authors suggested that maintenance schemes based on TBW should be the same as those for non-obese patients without an apparent risk for accumulation. The lack of a clear increase in the initial distribution volume might suggest adjusting the initial induction bolus to avoid overdosing and consequent hemodynamic repercussions. In line with this result Ingrande et al. [65] found that scaling the induction bolus of propofol to lean mass was more appropriate than TBW. In a study by our group [17] we studied 19 morbidly obese patients who received propofol and remifentanil based anesthesia. Plasma concentrations in these patients were analyzed, along with data from two other studies in morbidly obese patients [30] and healthy volunteers [33]. In total 51 subjects with a wide range of BMI (16–52 kg/m2) were included. In this study we found that a 3-compartment model, using TBW to allometrically scale volumes and clearances was superior to other size descriptors (FFM, LBM, NFM). Later studies [18, 66, 67] support the allometric relationship to TBW as a valid alternative for propofol dose adjustment in the obese. According to these new models the infusion rates of propofol during anesthetic maintenance (mg/kg/h) should be reduced nonlinearly with increasing body weight. Of the various models available, that developed by Eleveld et al. [18] deserves special mention, as it is derived from a large population of 660 individuals and 21 studies, to help estimate volumes and clearances, and the impact of other covariates besides body weight (such as age, sex, and gender).
Propofol TCI with the Marsh and Schnider Models in the Obese
Commercially available TCI pumps use the Marsh [36] and Schnider [33] propofol models which were derived from non-obese patients. When prospectively tested in obese patients both models have shown poor performance [68, 69]. Extrapolation of model predictions from a model derived from one population to another of different qualities (i.e., age, weight or disease) is not advisable since it carries the risk of important misspecifications and dosing errors.
The Marsh Model
The Marsh model scales all of its volumes and clearances to total body weight . Consequently, it delivers twice the dose in mg or mg/h, to a patient who weighs double that of another, without adjustment by other covariates. As mentioned above, it is evident that the clearance of a drug does not increase in proportion to body weight and thus this model will most likely administer an excess of drug with increasing magnitude according to degree of obesity. In turn, the central volume, a key parameter in the calculation of the initial bolus, will be overestimated in the obese patient generating a comparatively large bolus [69]. The use of the Marsh model for TCI in obese patients remains controversial [70]. Some studies suggest that, if used, anesthetic maintenance dose should be determined without weight correction [68, 71], whilst others recommend using ABW instead [29]. This last approach allows for a reduction in bolus size and maintenance dose, without the need to adjust the target concentration. We believe that using Marsh with ABW is a better alternative, nevertheless, due to model misspecifications from linear per kg assumptions, propofol administration should always be titrated using an EEG monitor to assure adequate anesthetic depth.
Related posts:
Full access? Get Clinical Tree
