Study objective
Well-designed graphs can portray complex data and relationships in ways that are easier to interpret and understand than text and tables. Previous investigations of reports of clinical research showed that graphs are underused and, when used, often depict summary statistics instead of the data distribution. This descriptive study aims to evaluate the quantity and quality of graphs in the current medical literature across a broad range of better journals.
Methods
We performed a cross-sectional survey of 10 randomly selected original research articles per journal from the 2012 issues of 20 highly cited journals. We identified which figures were data graphs and limited analysis to a maximum of 5 randomly selected data graphs per article. We then described the graph type, data density, completeness, visual clarity, special features, and dimensionality of each graph in the sample.
Results
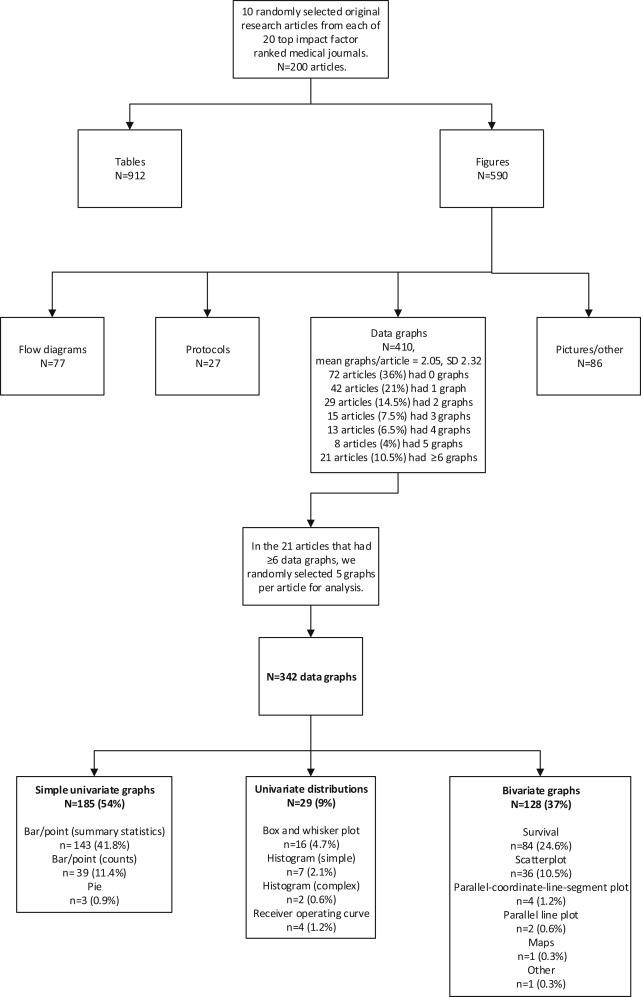
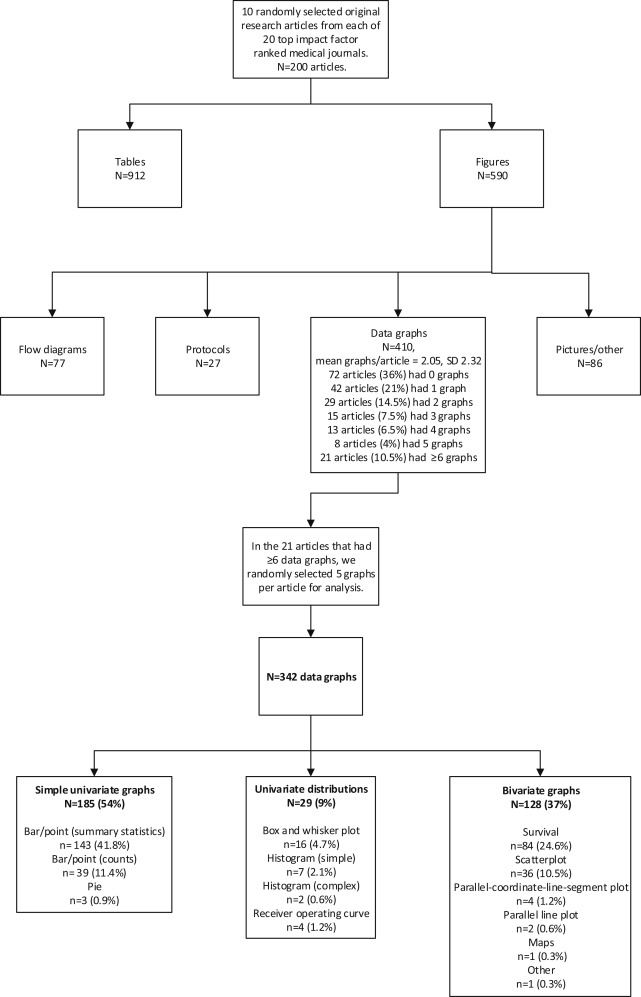
We analyzed 342 data graphs published in 20 journals. Our sample had a geometric mean data density index across all graphs of 1.18 data elements/cm 2 . More than half (54%) of the data graphs were simple univariate displays such as line or bar graphs. When analyzed by journal, excellence in one domain (completeness, visual clarity, or special features) was not strongly predictive of excellence in the other domains.
Conclusion
Despite that graphs can efficiently and effectively convey complex study findings, we found their infrequent use and low data density to be the norm. The majority of graphs were univariate ones that failed to display the overall distribution of data.
Introduction
Clinical investigators face a dilemma when it comes time to report their research; they have far more data than can be presented in a typical print publication. Graphs can present the data more efficiently than text alone and in a visual format that is particularly powerful. Well-designed graphs can portray complex data and relationships in ways that are easier to interpret and understand than text and tables alone. However, previous investigations demonstrate that many articles lack graphs, and those that do contain them generally only have basic formats, depicting summary statistics without measures of precision. Previous research also demonstrated that graphs rarely depict the underlying distribution of data, lack presentation of by-subject data, fail to show paired data when the design included paired measurements, and do not use symbolic dimensionality to convey additional variables in the data.
What is already known on this topic
Data graphs in medical journals are common but vary greatly in their design and use. How those variables may differ in various leading medical journals has not been previously reported.
What question this study addressed
Three hundred forty-two graphs in 20 leading medical journals in various specialties were assessed for types of graphs published, data density, completeness, visual clarity, and special features.
What this study adds to our knowledge
More than half of all graphs were simple univariate displays (eg, line or bar graphs) and 44% did not meet the study completeness criteria. Journal excellence in one of the characteristics above did not necessarily demonstrate it in others; elite journals could be very strong in one parameter and weak in another.
How this is relevant to clinical practice
Although readers can be provided more and better information by well-designed graphs, in this study approximately half were univariate versions that failed to add much information value. There appears to be much room for improvement.
Research on medical journals’ instructions for authors indicates that only 13% of journals provide any instructions on the use of graphs. Another study at a single journal found that peer reviewers rarely commented on graphs, and the few changes in graphs that originated at the editorial level were generally cosmetic.
More than a decade ago, we analyzed graphs in Annals of Emergency Medicine , in the Journal of the American Medical Association (JAMA ), and in pharmaceutical advertisements. Since then, there have been improvements in the graphing capabilities of statistical software packages, updates to publication guidelines that encourage greater transparency and data sharing in research, and a proliferation of supplementary Web pages on many journals’ Web sites that give authors nearly unlimited space to show their data. However, it is not clear whether these advances have made differences in the quantity and quality of graphs in major medical journals. In this descriptive study, we aimed to evaluate the quantity and quality of graphs in the current medical literature across a broad range of journals. This information could help authors and editors compare the quality of their graphs to those of the other journals analyzed and encourage both authors and editors to pay more attention to this important topic.
Materials and Methods
Selection of Articles and Graphs
We performed a cross-sectional survey of graphs in journals with high impact factors. In accordance with our experience with similar projects, we decided that 10 articles per journal from 20 highly cited journals would provide a reasonable accounting of the state of the literature. Using the 2011 Institute for Scientific Information rankings, we identified the institute’s 6 top-ranked general medical journals, its highest-ranked journals in 6 core specialties, and its 8 highest-ranked journals in randomly selected medical and surgical subspecialty journals that publish clinical research. We then performed a PubMed search for each selected journal to generate a list of potential articles published in 2012, exported them to a database, randomized their order with Stata (version 12.0; StataCorp, College Station, TX), and progressed through the list from top to bottom until we identified 10 original clinical research articles that studied at least 40 patients. We excluded research letters, meta-analyses, reviews, nonhuman studies, and other original publications that were a synthesis of other research (eg, cost-effectiveness analyses, decision analyses) to focus on reports of human observational studies and trials. All articles were obtained electronically as PDF files of the full, final, online version from the journal Web sites, including any supplementary tables and figures.
For each of the 10 articles from each journal, we first identified the number of tables and figures in the article and any supplemental material. For our analysis, we included only figures that were data graphs, excluding figures that represented protocol depictions, Consolidated Standards of Reporting Trials–type flow figures, photographs, or diagrams. To avoid having an atypical article dominate our descriptive statistics, we limited the analysis to a maximum of 5 data graphs per article. For articles with more than 5 data graphs, we selected 5 at random. If a data graph had more than 1 part, eg, Figure 1 A , B , and C , we separated them (considering them as 3 independent graphs) unless the graphs shared at least 1 common axis, such as with small multiples, in which case it was counted as 1 figure. We then described the graph type, data density, completeness, visual clarity, and special features of each graph in the sample ( Figure E1 , available online at http://www.annemergmed.com ).
Definitions: Graph Types
We defined the graph type as “simple” for univariate graphs including bar, line, point, and pie charts. We defined it as “intermediate” for univariate distributions including histograms and box and whisker plots. Finally, we defined it as “complex” for bivariate graphs, defined as scatter plots, parallel line plots, survival curves, and other depictions that showed paired data.
Development and Definition of Scoring Elements
We developed the scoring rules for the graph evaluation according to previous work. We first tested the rules and assessed interrater reliability by having each rater-author independently score a training set of 20 graphs from selected 2012 articles not included in this report. We achieved 80% to 95% agreement. Additional reviewers were trained with coding rules and explanatory materials, as listed in Figures E2 through E4 (available online at http://www.annemergmed.com ) and evaluated by their performance in scoring the same set of 20 graphs. Reviewers, who had already performed this task in a related effort, used a 99-item electronic abstraction form (Excel [version 14.0; Microsoft, Redmond, WA]) developed to characterize the quality of each graph. The spreadsheet had an embedded codebook for each item and had built-in error checking to ensure adherence with the scoring rules and enhance reliability. Graphs were generally rated by a single reviewer only, with areas of controversy adjudicated by consensus of the authors. Reviewers were also free to seek the advice of senior authors anytime there was a question.
We chose objective criteria of quality on the basis of the important elements of graph design outlined by Tufte, as well as our previous work. The characteristics we abstracted from each graph encompassed 5 content areas: data density, completeness, visual clarity, special features, and dimensionality.
We calculated the data density index, which quantifies the average amount of information per square centimeter in a graph. In theory, high-quality graphs should have a data density greater than text to justify their existence. The denominator of the data density index is the number of square centimeters the graph occupies in the print journal. The numerator is the amount of information displayed. For example, in a bar graph showing the means of 3 groups, each bar is scored as 2 points, the height of the bar and the bar’s identifier. Each point in a scatter plot is given 3 points, an x value, a y value and the link between them. Detailed scoring rules have been described ( Figure E2 , available online at http://www.annemergmed.com ).
“Completeness” describes a graph that has all the elements necessary for the graph to be self-explanatory. We defined a graph as complete if it was appropriately titled and labeled, all data elements were defined, variance and numbers at risk were depicted when appropriate, and the N for the data element was portrayed if not self-evident. “Distortion” refers to problems arising from improperly scaled axes or improperly ranged ones. “Chart junk” includes visual problems such as unnecessary grid lines, moiré patterns, or other extra ink that compromises the reader’s ability to see the data. “Readability” addresses concerns with graphic elements such as labels or symbols, ensuring that they are of adequate size and arrangement to be easily read. “Other” issues include graphs that would be improved if rotated 90 degrees and improperly connected points. We then grouped the absence of distortion, chart junk, readability, and other issues under the rubric of “visual clarity.” “Special features” included the use of small multiples, the illustration of pairing, and the use of symbolic dimensionality. We calculated dimensionality as an indicator of the complexity of the graph. For example, a scatter plot has 2 dimensions ( x and y ), but if each point also has a symbol (eg, ♂ versus ♀) and color (eg, comorbidity versus none), that would be 4 dimensions because each individual has 4 linked qualities ( Figure E3 , available online at http://www.annemergmed.com ).
Data Management and Analysis
Data were transferred to Stata (version 14.0), which we used for data cleaning, analysis, and graph creation. Our goal was descriptive to characterize the quality of graphs in major medical journals in 2012. Our outcomes included the data density index, graph type, completeness, visual clarity, use of special features, and dimensionality.
Because the data density index data had a wide range, we chose to analyze log data density index and then report geometric means. A geometric mean is the mean of the log data density indexes transformed back. We also stratified the data density index by graph type to investigate whether differences in journals’ data density indexes were due to the types of graphs they were publishing.
Materials and Methods
Selection of Articles and Graphs
We performed a cross-sectional survey of graphs in journals with high impact factors. In accordance with our experience with similar projects, we decided that 10 articles per journal from 20 highly cited journals would provide a reasonable accounting of the state of the literature. Using the 2011 Institute for Scientific Information rankings, we identified the institute’s 6 top-ranked general medical journals, its highest-ranked journals in 6 core specialties, and its 8 highest-ranked journals in randomly selected medical and surgical subspecialty journals that publish clinical research. We then performed a PubMed search for each selected journal to generate a list of potential articles published in 2012, exported them to a database, randomized their order with Stata (version 12.0; StataCorp, College Station, TX), and progressed through the list from top to bottom until we identified 10 original clinical research articles that studied at least 40 patients. We excluded research letters, meta-analyses, reviews, nonhuman studies, and other original publications that were a synthesis of other research (eg, cost-effectiveness analyses, decision analyses) to focus on reports of human observational studies and trials. All articles were obtained electronically as PDF files of the full, final, online version from the journal Web sites, including any supplementary tables and figures.
For each of the 10 articles from each journal, we first identified the number of tables and figures in the article and any supplemental material. For our analysis, we included only figures that were data graphs, excluding figures that represented protocol depictions, Consolidated Standards of Reporting Trials–type flow figures, photographs, or diagrams. To avoid having an atypical article dominate our descriptive statistics, we limited the analysis to a maximum of 5 data graphs per article. For articles with more than 5 data graphs, we selected 5 at random. If a data graph had more than 1 part, eg, Figure 1 A , B , and C , we separated them (considering them as 3 independent graphs) unless the graphs shared at least 1 common axis, such as with small multiples, in which case it was counted as 1 figure. We then described the graph type, data density, completeness, visual clarity, and special features of each graph in the sample ( Figure E1 , available online at http://www.annemergmed.com ).
Definitions: Graph Types
We defined the graph type as “simple” for univariate graphs including bar, line, point, and pie charts. We defined it as “intermediate” for univariate distributions including histograms and box and whisker plots. Finally, we defined it as “complex” for bivariate graphs, defined as scatter plots, parallel line plots, survival curves, and other depictions that showed paired data.
Development and Definition of Scoring Elements
We developed the scoring rules for the graph evaluation according to previous work. We first tested the rules and assessed interrater reliability by having each rater-author independently score a training set of 20 graphs from selected 2012 articles not included in this report. We achieved 80% to 95% agreement. Additional reviewers were trained with coding rules and explanatory materials, as listed in Figures E2 through E4 (available online at http://www.annemergmed.com ) and evaluated by their performance in scoring the same set of 20 graphs. Reviewers, who had already performed this task in a related effort, used a 99-item electronic abstraction form (Excel [version 14.0; Microsoft, Redmond, WA]) developed to characterize the quality of each graph. The spreadsheet had an embedded codebook for each item and had built-in error checking to ensure adherence with the scoring rules and enhance reliability. Graphs were generally rated by a single reviewer only, with areas of controversy adjudicated by consensus of the authors. Reviewers were also free to seek the advice of senior authors anytime there was a question.
We chose objective criteria of quality on the basis of the important elements of graph design outlined by Tufte, as well as our previous work. The characteristics we abstracted from each graph encompassed 5 content areas: data density, completeness, visual clarity, special features, and dimensionality.
We calculated the data density index, which quantifies the average amount of information per square centimeter in a graph. In theory, high-quality graphs should have a data density greater than text to justify their existence. The denominator of the data density index is the number of square centimeters the graph occupies in the print journal. The numerator is the amount of information displayed. For example, in a bar graph showing the means of 3 groups, each bar is scored as 2 points, the height of the bar and the bar’s identifier. Each point in a scatter plot is given 3 points, an x value, a y value and the link between them. Detailed scoring rules have been described ( Figure E2 , available online at http://www.annemergmed.com ).
“Completeness” describes a graph that has all the elements necessary for the graph to be self-explanatory. We defined a graph as complete if it was appropriately titled and labeled, all data elements were defined, variance and numbers at risk were depicted when appropriate, and the N for the data element was portrayed if not self-evident. “Distortion” refers to problems arising from improperly scaled axes or improperly ranged ones. “Chart junk” includes visual problems such as unnecessary grid lines, moiré patterns, or other extra ink that compromises the reader’s ability to see the data. “Readability” addresses concerns with graphic elements such as labels or symbols, ensuring that they are of adequate size and arrangement to be easily read. “Other” issues include graphs that would be improved if rotated 90 degrees and improperly connected points. We then grouped the absence of distortion, chart junk, readability, and other issues under the rubric of “visual clarity.” “Special features” included the use of small multiples, the illustration of pairing, and the use of symbolic dimensionality. We calculated dimensionality as an indicator of the complexity of the graph. For example, a scatter plot has 2 dimensions ( x and y ), but if each point also has a symbol (eg, ♂ versus ♀) and color (eg, comorbidity versus none), that would be 4 dimensions because each individual has 4 linked qualities ( Figure E3 , available online at http://www.annemergmed.com ).
Data Management and Analysis
Data were transferred to Stata (version 14.0), which we used for data cleaning, analysis, and graph creation. Our goal was descriptive to characterize the quality of graphs in major medical journals in 2012. Our outcomes included the data density index, graph type, completeness, visual clarity, use of special features, and dimensionality.
Because the data density index data had a wide range, we chose to analyze log data density index and then report geometric means. A geometric mean is the mean of the log data density indexes transformed back. We also stratified the data density index by graph type to investigate whether differences in journals’ data density indexes were due to the types of graphs they were publishing.

Full access? Get Clinical Tree




